八、基数排序(Radix Sort)
基数排序原理类似于桶排序。
假设要对10个在0~999范围内的数排序。一般来说,这是在0~bp-1范围内的N个数,b是基底,p是某个常数 。显然不能使用桶排序,这样使用的桶太多了。诀窍在于使用几趟桶式排序。比较简单的做法是从最低有效位开始(LSD)。
以b=10为例,这里只需要10个桶,多次使用。
先从个位数开始进行桶排序,可能不止一个数落到同一个桶里,把落到同一个桶里的数放到一个表里。每一趟都是稳定的:例如,进行了个位数的排序后,顺序取出,再按十位数装桶时,若十位数相等的话,个位数是按从小到大的顺序入桶的,即入完桶还是有序的。
步骤:
1)以个位数的值进行装桶;
2)将桶里的数字顺序取出来;
3)以十位数的值进行装桶;
4)顺序取出,再按百位......进行装桶。
eg.
数组{362,214,259,88,116,234}

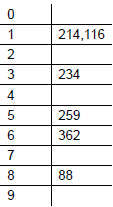

(从左至右依次是按个、十、百位数进行装桶的结果)
按个位数排序后,顺序取出{362,214,234,116,88,259};
按十位数排序后,顺序取出{214,116,234,259,362,88};
按百位数排序后,顺序取出{88,116,214,234,259,362};
排序完成。
计算数组中数值的最大位数:


/*** 计算输入数据中值的最大位数*/int maxBit(vector &a){ int bit = 0; for (int i = 0; i < a.size(); i++) { int p = a[i]; int c = 1; while (p / 10) { p = p / 10; c++; } if (c > bit) bit = c; } return bit;} 

1 void radix_sort(vector &a) 2 { 3 int buckets[10] = { 0 }; // 待排序数以10为基底,准备10个桶 4 int tmp[12]; 5 int bit = maxBit(a); // 计算待排序数的最大位数 6 int c = 1; 7 8 // 按位数操作,从个位开始,共进行bit次排序 9 for (int i = 0; i < bit; i++)10 {11 /* 桶要多次使用,装桶之前要清零 */12 for (int i = 0; i < 10; i++) 13 buckets[i] = 0;14 15 /* 按位进行桶排序 */16 for (int j = 0; j < a.size(); j++) 17 {18 int k = a[j] / c;19 int q = k % 10;20 buckets[q]++;21 }22 23 /* 将经过一轮桶排序后的数字顺序取出 */24 for (int i = 1; i < 10;i++)25 {26 buckets[i] += buckets[i - 1];27 }28 29 for (int j = a.size() - 1; j >= 0; j--)30 {31 int p = a[j] / c;32 int k = p % 10;33 tmp[buckets[k] - 1] = a[j];34 buckets[k]--;35 }36 37 /* 将tmp中的数拷回到a中,完成该回合排序 */38 for (int i = 0; i < a.size(); i++)39 {40 a[i] = tmp[i];41 }42 43 c = c * 10; // 位数向前挪一位44 }45 } 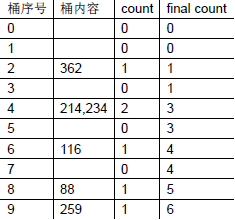
/** * 将一趟桶排序后的结果顺序取出 */ for(int i=1;i<10;i++) buckets[i] += buckets[i-1];for (int j = a.size() - 1; j >= 0; j--){ int p = a[j] / c; int k = p % 10; tmp[buckets[k] - 1] = a[j]; buckets[k]--;} - 表中的count表示该桶中数字的个数,也代表该桶会被分配到几个tmp的index索引
- final count(对应程序中的buckets[k])代表了该桶中数字分配到的最大的index加1,index=buckets[k]-1。如214,234占据了tmp的前3(final count)个位置,即1和2分别是214,234的索引
- 从后向前,先把234放到tmp[2](index为2),将buckets[k]减1,把214放到tmp[1](index为1)
时间复杂度:
算法运行时间O(p(N+b))
N:待排序的元素的个数
b:基底,也即桶的个数
p:待排序数的最大位数,也即排序进行的趟数